云玩家

本篇文章是 OpenAI Spinnging Up 中 Part 3: Intro to Policy Optimization 中代码的学习笔记, 原文在 https://spinningup.openai.com/en/latest/spinningup/rl_intro3.html , 代码在 https://github.com/openai/spinningup/blob/master/spinup/examples/pytorch/pg_math/1_simple_pg.py . 先给出代码 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711 ...

这里只是列出我在学习过程中出现的各种错误以及解决方法, 并不代表我了解报错产生的原因以及解决的原理, 所以可能有时候并不起效. 在这里 xxxx 代表任意字符串 (避免出现每个人的报错因路径或其他原因而不同, 但是相同的字符串一般会给出) , ... 代表大段字符串. 1. 报错 123456789usage: ipykernel_launcher.py [-h] [--env_name ENV_NAME] [--render] [--lr LR]ipykernel_launcher.py: error: unrecognized arguments: -f xxxx.jsonAn exception has occurred, use %tb to see the full traceback.SystemExit: 2xxxx/anaconda3/lib/python3.7/site-packages/IPython/core/interactiveshell.py:xxxx: UserWarning: To exit: use 'exit', 'qu ...

这份指南会将我遇到的 pytorch api 的作用都记录下来, 因此内容会不断更新. 某些非常常用并且简单的就不会在这里列出, 比如说 torch.tensor . torch.distributionstorch.distributions.categoricaltorch.distributions.categorical.Categorical CLASS 1torch.distributions.categorical.Categorical(probs=None, logits=None, validate_args=None) 依据参数 probs 与 logits 来采样. 例子: 1234567891011m = Categorical(torch.tensor([0.25, 0.25, 0.25, 0.25]))m.sample() # 在 0, 1, 2, 3 中等概率采样输出: tensor(3)m = Categorical(torch.tensor([[0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.2 ...

推导最简单的策略梯度我们考虑一个随机的, 参数化的策略 $\pi_{\theta}$ . 我们的目标是最大化期望回报 (还可以称为性能函数, 与损失函数意义相反) $J(\pi_{\theta})=\mathop{\mathrm{E}}\limits_{\tau\sim \pi_{\theta}}[R(\tau)]$ . 这里使用有限无折损回报 ($\textrm{finite-horizon undiscounted return}$) 来推导, 但是无限有折损回报 ($\textrm{infinite-horizon discounted return}$) 的推导几乎是完全相同的. 我们会用梯度下降 ($\textrm{gradient ascent}$) 来优化策略的参数, 比如$$ \theta_{k+1}=\theta_k+\alpha\nabla_{\theta}J(\pi_{\theta})|_{\theta_k} $$其中 $\nabla_{\theta}J(\pi_{\theta})|_{\theta_k}$ 代表 $\theta$ 取值为 $\theta_k$ . ...

一问题设 $M=\left[\begin{matrix}A&B\\\\C&D\end{matrix}\right]$ 为一个 $2n\times2n$ 矩阵, 其中每一块为一个 $n\times n$ 矩阵. 假设 $A$ 可逆且 $AC=CA$ . 那么有 $\det M=\det(AD-CB)$ . 证明由于 $A$ 可逆且 $AC=CA$ , 所以两边左乘 $A^{-1}$ 有 $C=ACA^{-1}$ . 那么有$$ \begin{aligned} \det\left[\begin{matrix}A&B\\\\C&D\end{matrix}\right]&=\det\left[\begin{matrix}A&B\\\\C-A(CA^{-1})&D-B(CA^{-1})\end{matrix}\right]\\\\ &=\det\left[\begin{matrix}A&B\\\\0&D-B(CA^{-1})\end{matrix}\right]\\\\ &=\det(A)\det \Big(D-B(CA^{-1})\Big)\\\\ &=\det\Big(D-B(CA^{-1} ...

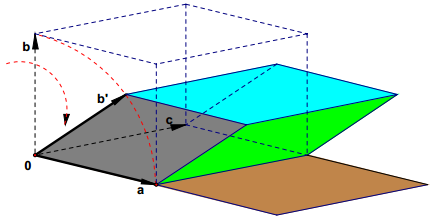
行列式具有良好的性质, 通常它是线性代数中较为基本的内容. 而行列式有非常直观的几何性质, 其绝对值是以矩阵中的向量为棱的在标准正交基下的平行四边形 (六面体) 的体积, 当维数超过三维时, 有类似的结果, 我们可以称其为 “广义平行六面体” 的体积. 我们给出广义平行六面体体积的一个递归定义. 设 $A$ 为 $n\times n$ 矩阵, 其中第 $k$ 行向量 $L$ 即为广义平行六面体 $V$ 的一个棱,$$ \newcommand\xrule{\rule[.5ex]{2em}{.4pt}} \left[\begin{matrix} &\vdots&\\\\ \xrule& L_k&\xrule\\\\ &\vdots& \end{matrix}\right] $$以 $L_2,L_3,\dots L_n$ 为平行六面体 $V$ 的底, 而以 $L_1$ 正交于 $L_2,L_3,\dots L_n$ 的分量 $H$ 作为 $V$ 的高, 将 $L_1$ 分为两个正交分量 $H$ 与 $G$, 而 $G$ 可以被 $L_2,L_3,\dots L_n$ 线性表示, 那么就有$ ...

数值梯度 (Numerical Gradient)$$ \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\\\\ \frac{\mathrm{d}f(x)}{\mathrm{d}x}\approx\frac{f(x+\epsilon)-f(x-\epsilon)}{2\epsilon} $$ 根据上式, 当 $\epsilon$ 取得足够小时, 就可以近似的认为其是梯度. 这样的方法求梯度非常方便, 但是并不是完全精确 (总是存在误差) , 这就是数值梯度. 解析梯度 (Analytical Gradient)解析梯度即利用求导法则, 精确的求出其梯度, 推导一般比较麻烦, 但是如果推导出来, 那么求梯度的速度和精确度会好于数值梯度 例子比如说我们要求 $f(x)=x^2$ 这个函数在 $x=2$ 时的梯度. 数值梯度$$ \left.\frac{\mathrm{d}f(x)}{\mathrm{d}x}\right|_{x=2}\appro ...

简介相信大家都在高中接触过超几何分布. 超几何分布是不放回的, 该分布给出了抽取 $n$ 次后抽到次品次数的概率. 如果一个随机变量 $X$ 服从于超几何分布, 那么有$$ P(X=k)=\frac{C_{N}^kC_{M-N}^{n-k}}{C_{M}^{n}} $$其中 $k$ 为抽取到的次品数, $M$ 为总数, $N$ 为总次品数. 问题生活中很多变量都服从于超几何分布, 我们举个例子 假设你们班要选出 $10$ 个人参加某个活动, 但是想要参加活动的人却有 $40$ 个人, 那么就要采取抽纸条的方式来选出参加活动的人. 准备 $40$ 张纸条, 其中有 $10$ 张是被标记了的. $40$ 个候选人每人抽取一张纸条, 抽到被标记纸条的人就可以参加活动. 当已经有 $n$ 个人抽取了之后, $n$ 个人里面有 $X$ 个人可以参加活动, 这个 $X$ 就服从于超几何分布. 现在我们想要讨论的问题是: 这样的抽取公平吗? 先抽和后抽对你抽到标记纸条的概率有没有影响? 再抽象一点, 即如果第 $n$ 次抽取时, 前面 $n-1$ 次抽取的结果都未知, 那么这次抽取抽到次品的概率 ...

有模型与无模型强化学习的一个最重要的分支即为有模型 ($\textrm{Model-Base}$) 与无模型 ($\textrm{Model-Free}$) 学习. 它们的区别在于, 代理人 ($\textrm{Agent}$, 即执行算法的主体) 是否获得环境的模型 ($\textrm{Model}$). 有了模型, 就可以预知状态转移以及回报. 有模型有模型能够让代理人在做出决策前先思考, 看看在做出某个可能的动作后会发生什么, 并在可能的动作中选择出确切的决策. 与无模型相比, 能够大大提高样本效率 ($\textrm{sample efficiency}$, 你从每条样本中得到的越多, 样本效率就越高, 详情可见 What is sample efficiency?). 但是有模型学习同样也有缺点, 得到一个很好描述现实的模型通常是不可能的. 并且代理人有可能在模型上学到一些 “偏见” (可以类比监督学习中的过拟合), 这使得代理人在模型中表现德很好, 但是在真实环境中表现并不是很好 (甚至很差) . 无模型无模型就比较好介绍了, 就是没有这个模型. 如何学习无模型参数优化 ...

本魔改主题适用 Hexo 4 . 所有魔改均可取消! 配置默认不开启, 因此可以平滑换到魔改 butterfly 主题. 首先推介 butterfly 文档, 这里只介绍魔改部分的配置. 这里的示例仅为合法示例, 即你填了该示例不一定能正确显示, 仅供参考. 魔改主题 Github 地址 使用主题 & 平滑更换下载并配置进入主题目录, 下载主题 1git clone https://github.com/cnyist/hexo-modify-theme-butterfly.git 将下载下来的主题文件夹名字改为 Butterfly , 同时修改hexo配置文件_config.yml，把主題改为Butterfly 1theme: Butterfly 如果你没有 pug 以及stylus的渲染器, 请下载安装: 1npm install hexo-renderer-pug hexo-renderer-stylus --save or 1yarn add hexo-renderer-pug hexo-renderer-stylus 如果你之前不是使用 butterfly 主题, ...