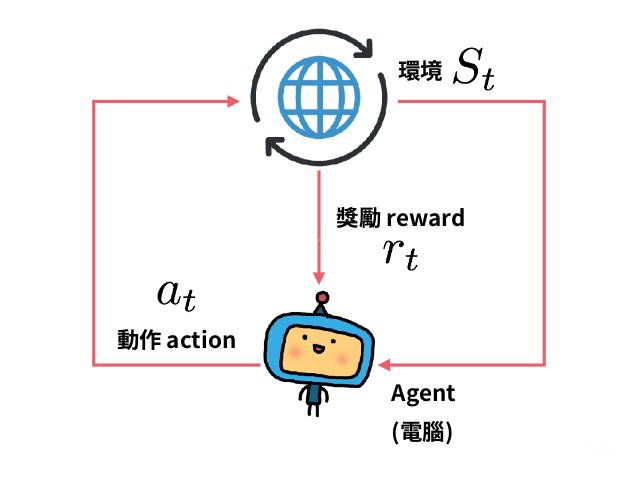
参数优化

推导最简单的策略梯度

我们考虑一个随机的, 参数化的策略 ${\pi }_{\theta }$ . 我们的目标是最大化期望回报 (还可以称为性能函数, 与损失函数意义相反) $J({\pi }_{\theta })=\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[R(\tau )]$ . 这里使用有限无折损回报 ($\text{finite-horizon undiscounted return}$) 来推导, 但是无限有折损回报 ($\text{infinite-horizon discounted return}$) 的推导几乎是完全相同的.

我们会用梯度下降 ($\text{gradient ascent}$) 来优化策略的参数, 比如

$${\theta }_{k+1}={\theta }_k+\alpha {\mathrm{\nabla }}_{\theta }J({\pi }_{\theta }){|}_{{\theta }_k}$$

其中 ${\mathrm{\nabla }}_{\theta }J({\pi }_{\theta }){|}_{{\theta }_k}$ 代表 $\theta$ 取值为 ${\theta }_k$ .

为了使用该算法, 我们需要一个能够用数值计算的策略梯度表达式. 这包括两个步骤:

1. 推导出策略性能的解析梯度 ($\text{analytical gradient}$ , 什么是解析梯度? 详情看这篇文章) , 以期望值的形式表现 (便于用平均值估计).
2. 算出在样本上的估计的期望值, 可以使用有限步代理人-环境交互的数据.

这里列出对推导解析梯度有帮助的一些事实.

1. 轨迹的概率. 采取策略 ${\pi }_{\theta }$ 所做出的轨迹 $\tau =\{s_0,a_0,\dots ,s_{T+1}\}$ 的概率是

$$P(\tau \mid \theta )={\rho }_0(s_0)\prod _{t=0}^{T}P(s_{t+1}\mid s_t,a_t){\pi }_{\theta }(a_t\mid s_t)$$

1. 对数的把戏. 我们知道 $\log x$ 对 $x$ 的导数是 $1/x$ , 于是根据链式法则有

$${\mathrm{\nabla }}_{\theta }P(\tau \mid \theta )=P(\tau \mid \theta )\frac{1}{P(\tau \mid \theta )}{\mathrm{\nabla }}_{\theta }P(\tau \mid \theta )=P(\tau \mid \theta ){\mathrm{\nabla }}_{\theta }\log P(\tau \mid \theta )$$

1. 轨迹的对数概率

$$\log P(\tau \mid \theta )=\log {\rho }_0(s_0)+\sum _{t=0}^T(\log P(s_{t+1}\mid s_t,a_t)+\log {\pi }_{\theta }(a_t\mid s_t))$$

1. 环境函数的梯度. 由于 ${\rho }_0(s_0),P(s_{t+1}\mid s_t,a_t),R(\tau )$ 与 $\theta$ 都无关, 因此它们的梯度为 $0$ .
2. 由第 4 条与第 3 条可知, 轨迹的对数概率的梯度是

$$\begin{array}{rl}{\mathrm{\nabla }}_{\theta }\log P(\tau \mid \theta )& ={\mathrm{\nabla }}_{\theta }\log {\rho }_0(s_0)+\sum _{t=0}^T({\mathrm{\nabla }}_{\theta }\log P(s_{t+1}\mid s_t,a_t)+{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t))\\ \\ & =\sum _{t=0}^Y{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\end{array}$$

由以上全部推导就有

$$\begin{array}{rl}{\mathrm{\nabla }}_{\theta }J({\pi }_{\theta })& ={\mathrm{\nabla }}_{\theta }\underset{\tau \sim {\pi }_0}{\mathrm{E}}[R(\tau )]\\ \\ & ={\mathrm{\nabla }}_{\theta }{\int }_{\tau }P(\tau \mid \theta )R(\tau )\\ \\ & ={\int }_{\tau }{\mathrm{\nabla }}_{\theta }P(\tau \mid \theta )R(\tau )\\ \\ & ={\int }_{\tau }P(\tau \mid \theta ){\mathrm{\nabla }}_{\theta }\log P(\tau \mid \theta )R(\tau )\\ \\ & =\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log P(\tau \mid \theta )R(\tau )]\\ \\ & =\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)R(\tau )]\end{array}$$

这样我们就可以用样本的平均值来估计策略梯度了. 假如我们有轨迹的集合 $\mathcal{D}=\{{\tau }_i{\}}_{i=1,\dots ,N}$ , 并且这些轨迹都是代理人根据策略 ${\pi }_{\theta }$ 在环境中行动获得, 那么策略梯度可以估计为

$$\hat{g}=\frac{1}{|\mathcal{D}|}\sum _{\tau \in \mathcal{D}}\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)R(\tau )$$

其中 $|\mathcal{D}|$ 是集合 $\mathcal{D}$ 的元素个数.

损失函数

在强化学习中, 我们同样可以定义类似监督学习中的损失函数的概念, 但是在强化学习中的损失函数与监督学习中的损失函数有很大区别. 损失函数的梯度与策略梯度是相同的. 其接受的数据包含了 (状态, 动作, 权重) 三元组.

与参数关系

在监督学习中, 损失只与数据有关而与参数无关, 但是在强化学习中, 由于数据是遵循最近的策略采样得来的, 因此损失也与参数有关.

描述性能

在强化学习中, 我们关心的是期望回报 $J({\pi }_{\theta })$ , 而损失函数并不能很好的表达它. 最优化损失函数并不能保证能够提升期望回报. 你甚至可以将损失函数降低到 $-\mathrm{\infty }$ 而同时策略性能 (期望回报) 并不怎样. 此时我们称其 “过拟合” . 但这与我们通常所称的过拟合有所不同, 这只是一种描述, 因为实际上并没有什么泛化的错误, 只是损失函数低得吓人. 因此如果想真正描述策略性能, 我们应该关心期望回报而不是损失函数.

EGLP 定理

在这里我们会推导出一个在策略梯度中被广泛使用的一个中间结果, 我们称其为梯度对数概率期望 ($\text{Expect Grad-Log-Prob, EGLP}$) 定理.

$$\begin{array}{rl}{\int }_x{P}_{\theta }(x)& =1\\ \\ {\mathrm{\nabla }}_{\theta }{\int }_x{P}_{\theta }(x)& ={\mathrm{\nabla }}_{\theta }1\\ \\ {\mathrm{\nabla }}_{\theta }{\int }_x{P}_{\theta }(x)& =0\\ \\ {\int }_x{\mathrm{\nabla }}_{\theta }{P}_{\theta }(x)& =0\\ \\ {\int }_x{P}_{\theta }(x){\mathrm{\nabla }}_{\theta }\log P_{\theta }(x)& =0\\ \\ \underset{x\sim P_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log P_{\theta }(x)]& =0\end{array}$$

别让过去影响你

梯度更新表达式

$${\mathrm{\nabla }}_{\theta }J({\pi }_{\theta })=\underset{\tau \sim {\pi }_0}{\mathrm{E}}[\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_0(a_t\mid s_t)R(\tau )]$$

每次更新, 都可以让每个动作的对数概率随着 $R(\tau )$ (采取动作的总回报) 成比例增加. 但这意义不大. 代理人应该根据其采取行动后的后果 (好还是坏) 来决定如何更改 (加强) 策略, 而采取行动之前的奖励和这一步行动的好坏没有直接关系. 事实上, 这一直觉在数学上也有很好的表达. 可以证明, 梯度更新表达式也可以写成如下等价形式.

$${\mathrm{\nabla }}_{\theta }J({\pi }_{\theta })=\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\sum _{t^{\prime }=t}^{T}R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})]$$

这被称为奖励策略梯度 ($\text{reward-to-go policy gradient}$).

证明过程比较繁琐, 不想看的可以略过.

证明

我们先提出一个函数

$$\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[f(t,t^{\prime })]=\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})]$$

如果我们能证明当 $t'

$$\begin{array}{rl}\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[f(t,t^{\prime })]& ={\int }_{\tau }P(\tau \mid {\pi }_{\theta })f(t,t^{\prime })\\ \\ & ={\int }_{s_t,a_t,s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}}P(s_t,a_t,s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}\mid {\pi }_{\theta })f(t,t^{\prime })\\ \\ & =\underset{s_t,a_t,s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}\sim {\pi }_{\theta }}{\mathrm{E}}[f(t,t^{\prime })]\end{array}$$

根据贝叶斯法则, 我们有

$$\begin{array}{rl}\underset{A,B}{\mathrm{E}}[f(A,B)]& ={\int }_{A,B}P(A,B)f(A,B)\\ \\ & ={\int }_A{\int }_{B}P(B\mid A)P(A)f(A,B)\\ \\ & ={\int }_{A}P(A){\int }_{B}P(B\mid A)f(A,B)\\ \\ & ={\int }_{A}P(A)\underset{B}{\mathrm{E}}[f(A,B)|A]\\ \\ & =\underset{A}{\mathrm{E}}[\underset{B}{\mathrm{E}}[f(A,B)|A]]\end{array}$$

若 $f(A,B)=h(A)g(B)$ , 那么还有

$$\begin{array}{rl}\underset{A,B}{\mathrm{E}}[f(A,B)]& =\underset{A}{\mathrm{E}}[\underset{B}{\mathrm{E}}[f(A,B)|A]]\\ \\ & =\underset{A}{\mathrm{E}}[\underset{B}{\mathrm{E}}[h(A)g(B)|A]]\\ \\ & =\underset{A}{\mathrm{E}}[h(A)\underset{B}{\mathrm{E}}[g(B)|A]]\end{array}$$

因此就有

$$\begin{array}{rl}\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[f(t,t^{\prime })]& =\underset{s_t,a_t,s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}\sim {\pi }_{\theta }}{\mathrm{E}}[f(t,t^{\prime })]\\ \\ & =\underset{s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}\sim {\pi }_{\theta }}{\mathrm{E}}[\underset{s_t,a_t\sim {\pi }_{\theta }}{\mathrm{E}}[f(t,t^{\prime })|s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}]]\\ \\ & =\underset{s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}\sim {\pi }_{\theta }}{\mathrm{E}}[\underset{s_t,a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})|s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}]]\\ \\ & =\underset{s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}\sim {\pi }_{\theta }}{\mathrm{E}}[R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})\underset{s_t,a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)|s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}]]\end{array}$$

而

$$\begin{array}{r}\underset{s_t,a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)|s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}]={\int }_{s_t,a_t}P(s_t,a_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}){\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\end{array}$$

当 $t'

$$\begin{array}{rl}P(s_t,a_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})& =P(a_t\mid {\pi }_{\theta },s_t,a_{t^{\prime }},s_{t^{\prime }+1})P(s_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})\\ \\ & ={\pi }_{\theta }(a_t\mid s_t,a_{t^{\prime }},s_{t^{\prime }+1})P(s_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})\\ \\ & ={\pi }_{\theta }(a_t\mid s_t)P(s_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})\end{array}$$

这是因为 $a_t$ 在当前环境 $s_t$ 已知晓时, 与之前做过的选择与之前经历的环境并无关系.

因此有

$$\begin{array}{rl}\underset{s_t,a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)|s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}]& ={\int }_{s_t,a_t}P(s_t,a_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}){\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\\ \\ & ={\int }_{s_t,a_t}{\pi }_{\theta }(a_t\mid s_t)P(s_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}){\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\\ \\ & ={\int }_{s_t}P(s_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}){\int }_{a_t}{\pi }_{\theta }(a_t\mid s_t){\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\\ \\ & =\underset{s_t\sim {\pi }_{\theta }}{\mathrm{E}}[\underset{a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)|s_t]|s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1}]\end{array}$$

此时就要用到我们的 $\text{EGLP}$ 定理了.

$$\begin{gathered} \because {\int }_{a_t}{\pi }_{\theta }(a_t\mid s_t)|s_t=1 \\ \therefore \underset{a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)|s_t]=0 \end{gathered}$$

因此当 $t'

而当 $t^{\prime }⩾t$ 时, 无法将 $P(s_t,a_t\mid {\pi }_{\theta },s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})$ 分解成该形式, 所以就不会有这个结果. 我们可以举个例子. 如果现在有 $80\mathrm{\%}$ 的几率会下雨, 而你打算如果不下雨, 就有 $90\mathrm{\%}$ 的可能会出去买水果. 此时, 无论之前发生了什么 (也许昨天下雨了 (环境) , 也许前天买了水果 (动作)) , 现在买水果的概率都是 $(1-80\mathrm{\%})\times 90\mathrm{\%}=16\mathrm{\%}$ . 但是如果这个时候, 未来的你突然穿越回来, 告诉你你后来买了水果, 那么这时下雨的概率其实就改变了, 变得更倾向于不下雨 (事实上如果你后来买了水果, 不下雨的概率就会是 $1$ ). 如果没买, 则相反. 这就是未来影响现在而过去不影响现在.

既然期望是相同的, 但根据这个式子来训练为什么会更好呢? 这是因为策略梯度需要用样本轨迹来估计, 而且最好是低方差的. 如果方差较大, 说明估计不太准确. 如果公式中包括过去的奖励, 虽然它们均值为 $0$ , 但方差并不是, 在公式中增加它们只会给策略梯度的样本估计增加噪音, 增加方差. 而这会导致需要较多的样本轨迹才能得到一个相对稳定的值 (收敛) . 删除它们后, 我们就可以用更少的样本轨迹得到低方差的估计, 也就是说更容易收敛. 举个例子, 如果你要估计一系列数字的期望 (也就是算平均值) , 它们服从的概率分布的期望其实都是 $50$, 但是一个方差很大, 一会 $100$ 一会 $20$ 一会 $3$, 你需要很多数字才能得到一个较为准确的值. 而另一个方差很小, 基本就是 $50.3$ , $49.8$ , $49.5$ 这样, 只需要几个数字就能估计得差不多.

策略梯度的基线

由 $\text{EGLP}$ 可以得到一个非常直接的结论: 如果一个函数 $b(s_t)$ 只依赖于状态 $s_t$ , 那么有

$$\underset{a_t\sim {\pi }_{\theta }}{\mathrm{E}}[{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)b(s_t)]=0$$

这使得我们可以在策略梯度的表达式中任意加上 (或删除) 这样的项而不改变最终结果, 比如说

$$\begin{array}{rl}{\mathrm{\nabla }}_{\theta }J({\pi }_{\theta })& =\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)\sum _{t^{\prime }=t}^{T}R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})]\\ \\ & =\underset{\tau \sim {\pi }_{\theta }}{\mathrm{E}}[\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)(\sum _{t^{\prime }=t}^{T}R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})-b(s_t))]\end{array}$$

函数 $b$ 被称为基线 ($\text{baseline}$).

基线函数一般是策略上的价值函数 ($\text{on-policy value function}$) $V^{\pi }(s_t)$ . 稍微回想一下, 这个函数给出了代理人从状态 $s_t$ 开始, 使用策略 $\pi$ 以后的平均 (期望) 回报.

$$V^{\pi }(s)=\underset{\tau \sim \pi }{\mathrm{E}}[R(\tau )\mid s_0=s]$$

经验上, 让基线 $b(s_t)=V^{\pi }(s)$ 对降低策略梯度的样本估计的方差有好处, 这会让策略学习更快, 更稳定. 从概念上来看, 这也很有意义: 它体现了一个直觉, 如果代理人得到了它所期望的 (即 $\sum _{t^{\prime }=t}^{T}R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})=V^{\pi }(s)$) , 他会对此 “感到” 中立 ( “中立” 在数学上看来即值为 $0$ ).

事实上, $V^{\pi }(s_t)$ 并不能被准确计算, 因此应该使用它的估计. 通常我们会使用一个与策略同步更新 (这样就能总是估计最近的策略的价值函数) 的神经网络 $V_{\varphi }(s_t)$ 来估计它.

策略梯度的其他形式

我们已经见到了策略梯度的很多等价形式

$${\mathrm{\nabla }}_{\theta }J({\pi }_{\theta })=\underset{\tau \sim {\pi }_0}{\mathrm{E}}[\sum _{t=0}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_0(a_t\mid s_t){\mathrm{\Phi }}_t]$$

 ${\mathrm{\Phi }}_t$ 可以是

$${\mathrm{\Phi }}_t=R(\tau )$$

又或者

$${\mathrm{\Phi }}_t=\sum _{t^{\prime }=t}^{T}R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})$$

再或者

$${\mathrm{\Phi }}_t=\sum _{t^{\prime }=t}^{T}R(s_{t^{\prime }},a_{t^{\prime }},s_{t^{\prime }+1})-b(s_t)$$

但还有两种重要的形式.

1. 状态-动作价值函数

$${\mathrm{\Phi }}_t=Q^{{\pi }_{\theta }}(s_t,a_t)$$

证明可以看这里.

1. 优势方程

$${\mathrm{\Phi }}_t=A^{\pi }(s_t,a_t)$$

而

$$A^{\pi }(s_t,a_t)=Q^{\pi }(s_t,a_t)-V^{\pi }(s_t)$$

由基线得知等价.

为了更详细的了解这个主题, 你应该阅读 Generalized Advantage Estimation (GAE). 也可以参考我的文章 GAE 算法 .