《机器学习》 西瓜书习题 第 5 章: 神经网络
习题
5.1
试述将线性函数 $$f(\boldsymbol{x}) = \boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}$$ 用作神经元激活函数的缺陷.
理想中的激活函数是阶跃函数, 但是它不连续, 不光滑, 所以要一个连续、光滑的函数替代它. 线性函数虽然连续、光滑, 但是它跟阶跃函数并不是那么相似. 线性函数对 $$0$$ 周围的数值和对趋近 $$\infty$$ 的数值是一视同仁的, 而这样的性质我们并不需要, 我们更在乎那些处于 $$0$$ 周围的, 在被分为正 (大于 $$0$$ ) 还是负 (小于 $$0$$ ) 的界限边的 ‘模糊’ 的数值, 因此有了 $$\mathrm{Sigmoid}$$ 函数, 它的特点就是在 $$0$$ 周围输出急剧变化.
5.2
试述使用图 $$5.2(\mathrm{b})$$ 激活函数的神经元与对率回归的联系.
这已经非常明显了, 対率回归的激活函数也是 $$Sigmoid$$ .
5.3
对于图 $$5.7$$ 中的 $$v_{ih}$$ 试推导出 $$\mathrm{BP}$$ 算法中的更新公式 $$(5.13)$$ .
全部展开, 得
$$
\begin{aligned}
\Delta v_{ih} &= -\eta\frac{\partial E_k}{\partial b_h}\frac{\partial b_h}{\partial \alpha_h}x_i\\\\
&=-\eta\frac{\partial E_k}{\partial b_h}\frac{\partial b_h}{\partial \alpha_h}\frac{\partial \alpha_h}{\partial v_{ih}}\\\\
&=-\eta\frac{\partial E_k}{\partial v_{ih}}
\end{aligned}
$$
显然成立.
5.4
试述式 $$(5.6)$$ 中学习率的取值对神经网络训练的影响.
学习率太低, 训练速度太慢. 学习率太高, 不容易收敛 (在极值点附近反复迭代) .
5.5
试编实现标准 $$\mathrm{BP}$$ 算法和积累 $$\mathrm{BP}$$ 算法, 在西瓜数据集 $$3.0$$ 上分别用这两个算法训练一个单隐层网络, 并进行比较.
5.6
试设计一个 $$\mathrm{BP}$$ 改进算法, 能通过动态调整学习率显著提升收敛速度. 编程实现该算法, 并选择两个 $$\mathrm{UCI}$$ 数据集与标准 $$\mathrm{BP}$$ 算法进行实验比较.
简单描述一下, 就是一开始学习率比较高 (来更快逼近) , 然后学习率慢慢变小 (提高精度) ,
5.7
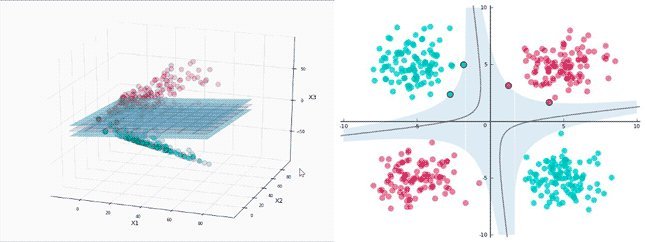
根据式 $$(5.18)$$ 和 $$(5.19)$$ , 试构造一个能解决异或问题的单层 $$\mathrm{RBF}$$ 神经网络.
5.8
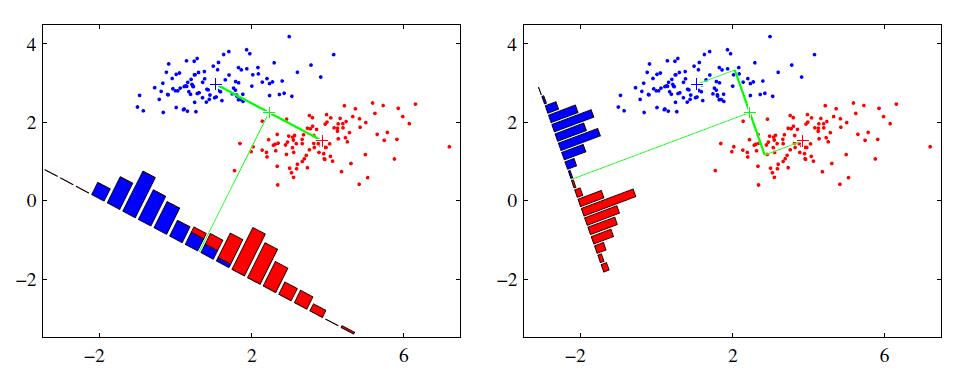
从网上下载或自己编程实现 $$\mathrm{SOM}$$ 网络, 并观察其在西瓜数据集 $$3.0\alpha$$ 上产生的结果.
5.9*
试推导用于 $$\mathrm{Elman}$$ 网络的 $$\mathrm{BP}$$ 算法.
说实话这个问题太变态了, 不过上网搜索一番总算是差不多弄懂了, 我自己估计说不清楚, 所以推荐零基础入门深度学习(5) - 循环神经网络.
5.10
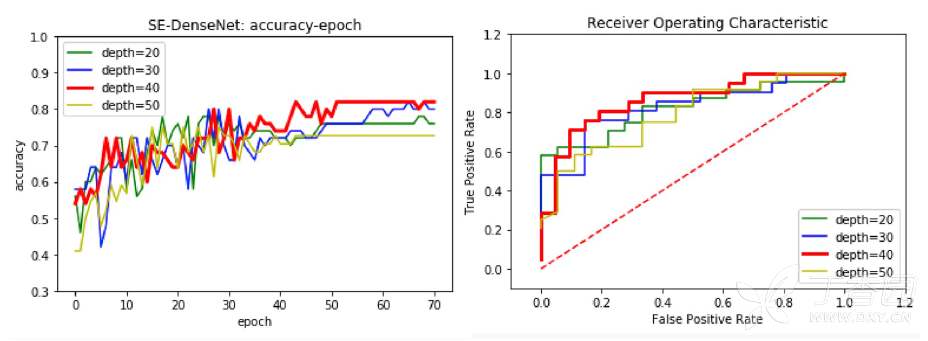
从网上下载或自己编程实现一个卷积神经网络, 并在手写字符识别数据 $$\mathrm{MNIST}$$ 上进行实验测试.