习题

6.1

试证明样本空间中任意点 $\boldsymbol{x}$ 到超平面 $(\boldsymbol{w}, b)$ 的距离为式 $(6.2)$ .

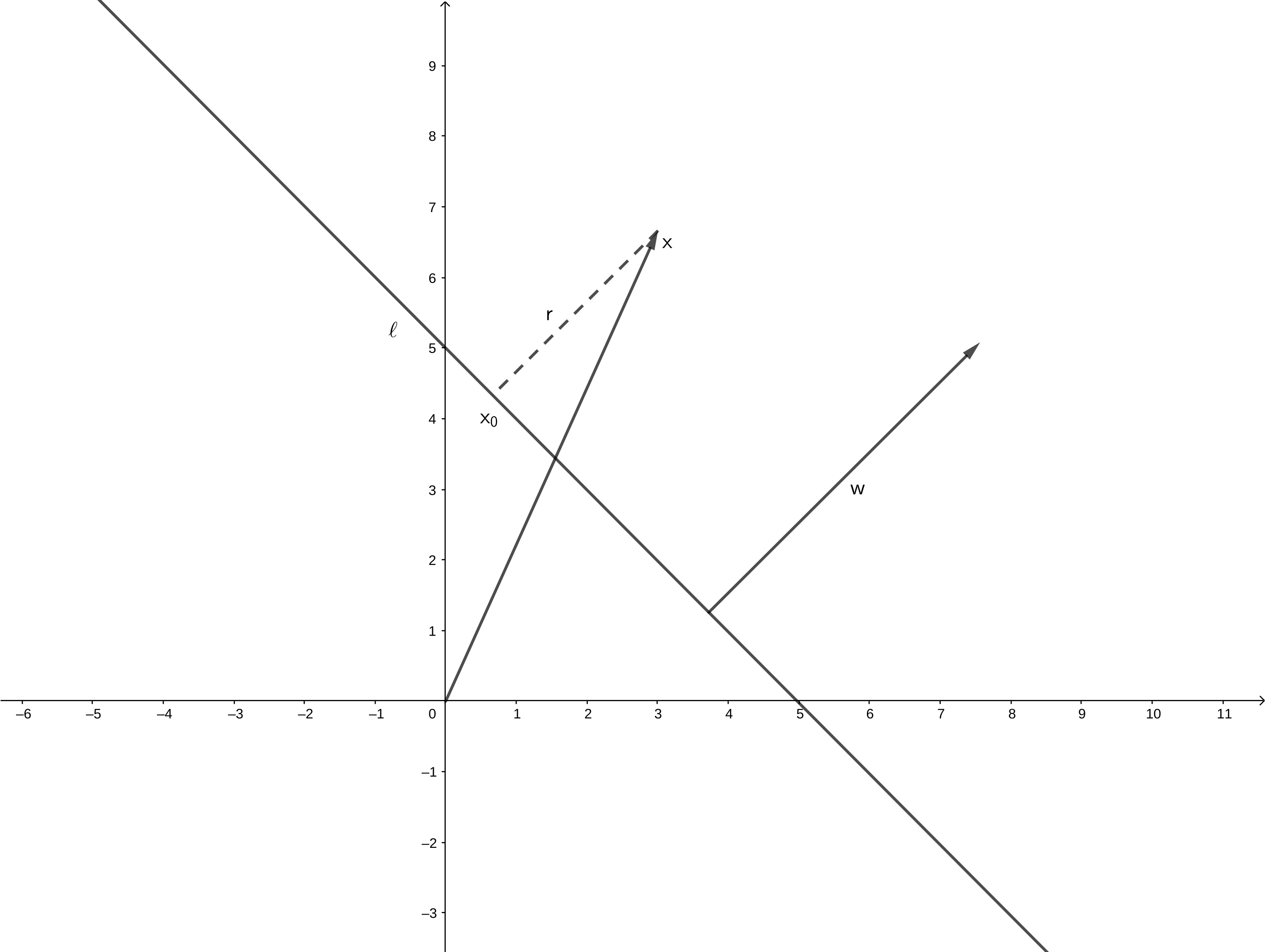
设超平面为 $\ell(\boldsymbol{w}, b)$ , $\boldsymbol{x}$ 在 $\ell$ 上的投影为 $\boldsymbol{x_0}$ , 离超平面的距离为 $r$ . 容易得
$$ \boldsymbol{w}\perp \ell\\\\\boldsymbol{x} = \boldsymbol{x_0} + r\frac{\boldsymbol{w}}{||\boldsymbol{w}||}\\\\\boldsymbol{w}^\mathrm{T}\boldsymbol{x_0} + b = 0 $$
则有
$$ \boldsymbol{x_0} = \boldsymbol{x} - r\frac{\boldsymbol{w}}{||\boldsymbol{w}||} $$

$$ \begin{aligned} \boldsymbol{w}^\mathrm{T}(\boldsymbol{x} - r\frac{\boldsymbol{w}}{||\boldsymbol{w}||}) + b &= 0\\\\ \boldsymbol{w}^\mathrm{T}\boldsymbol{x} - r\frac{\boldsymbol{w}^\mathrm{T}\boldsymbol{w}}{||\boldsymbol{w}||} + b &= 0\\\\ \boldsymbol{w}^\mathrm{T}\boldsymbol{x} - r\frac{||\boldsymbol{w}||^2}{||\boldsymbol{w}||} + b &= 0\\\\ \boldsymbol{w}^\mathrm{T}\boldsymbol{x} + b &= r\frac{||\boldsymbol{w}||^2}{||\boldsymbol{w}||}\\\\ \end{aligned} $$

即得
$$ r = \frac{\boldsymbol{w}^\mathrm{T}\boldsymbol{x} + b}{||\boldsymbol{w}||} $$
由于距离是大于等于 $0$ 的, 所以结果再加上绝对值
$$ r = \frac{\left|\boldsymbol{w}^\mathrm{T}\boldsymbol{x} + b\right|}{||\boldsymbol{w}||}\tag{6.2} $$

6.2

试使用 $\mathrm{LIBSVM}$ , 在西瓜数据集 $3.0\alpha$ 上分别用线性核和高斯核训练一个 $\mathrm{SVM}$ , 并比较其支持向量的差别.

《机器学习》西瓜书第 6 章编程实例

6.3

选择两个 $\mathrm{UCI}$ 数据集, 分别用线性核和高斯核训练一个 $\mathrm{SVM}$ , 并与 $\mathrm{BP}$ 神经网络和 $\mathrm{C4.5}$ 决策树进行实验比较.

《机器学习》西瓜书第 6 章编程实例

6.4

试讨论线性判别分析与线性核支持向量机在何种条件下等价.

线性判别分析能够解决 $n$ 分类问题, 而 $\mathrm{SVM}$ 只能解决二分类问题, 如果要解决 $n$ 分类问题要通过 $\mathrm{OvR(One\ vs\ Rest)}$ 来迂回解决.

线性判别分析能将数据以同类样例间低方差和不同样例中心之间大间隔来投射到一条直线上, 但是如果样本线性不可分, 那么线性判别分析就不能有效进行, 支持向量机也是.
综上, 等价的条件是:

数据有且仅有 2 种, 也就是说问题是二分类问题.
数据是线性可分的.

6.5

试述高斯核 $\mathrm{SVM}$ 与 $\mathrm{RBF}$ 神经网络之间的联系.

实际上都利用了核技巧, 将原来的数据映射到一个更高维的空间使其变得线性可分.

6.6

试析 $\mathrm{SVM}$ 对噪声敏感的原因.

$\mathrm{SVM}$ 的特性就是 “支持向量” . 即线性超平面只由少数 “支持向量” 所决定. 若噪声成为了某个 “支持向量” —— 这是非常有可能的. 那么对整个分类的影响是巨大的. 反观对率回归, 其线性超平面由所有数据共同决定, 因此一点噪声并无法对决策平面造成太大影响.

6.7

试给出试 $(6,52)$ 的完整 $\mathrm{KKT}$ 条件.

$\mathrm{KKT}$ 条件:
$$ \begin{cases} \xi_i \geqslant 0\\\\ \hat{\xi}_i \geqslant 0\\\\ f(\boldsymbol{x}_i) - y_i - \epsilon - \xi_i \leqslant 0\\\\ y_i - f(\boldsymbol{x}_i) - y_i - \epsilon - \hat{\xi}_i \leqslant 0\\\\ \mu_i \geqslant 0\\\\ \hat{\mu}_i \geqslant 0\\\\ \alpha_i \geqslant 0\\\\ \hat{\alpha}_i \geqslant 0\\\\ \mu_i\xi_i = 0\\\\ \hat{\mu}_i\hat{\xi}_i = 0\\\\ \alpha_i(f(\boldsymbol{x}_i) - y_i - \epsilon - \xi_i) = 0\\\\ \hat{\alpha}_i(y_i - f(\boldsymbol{x}_i) - y_i - \epsilon - \hat{\xi}_i) = 0 \end{cases} $$