如何快速搭建一个属于自己的网址导航
收藏夹内容太多, 有时候不方便找, 那么这时你就需要一个网址导航来放你的收藏夹的内容啦! 我知道理由很牵强, 反正就是要搭网址导航, 理由什么的自己去想. 这篇博文默认你已经注册了 Github .
Fork 网址导航项目项目地址
开启 Pages 服务
进入到你 Fork 后的仓库, 进入 Settings, 拉到下面开启 GitHub Pages.
此时, 你的网址导航已经成功建立, 可以根据上面的 “Your site is published at https://xxxx.xxx“
来进入你的网址导航. 如果要自定义域名, 可以在下面那个 “Custom domain” 框框里写上你自己的域名, 然后设置 CNAME 域名解析记录到 用户名.github.io . 就可以用你自己的域名访问网址导航了.
修改内容这个网址导航现在还不能算是你 “自己的” , 因此可以修改 index.html 来修改其成为你自己个性的网址导航. 修改的过程我就不细说了, 无非就是修改 favicon, title 这些的. 但是修改其中网址导航的网站可不是一件简单的工作, 一不留神就改错了, ...
手把手教你将博客备份到 Github
如果由于某些原因, 你把博客源文件弄丢了. 要是有备份, 那么就可以迅速恢复过来, 要是没有… 那你辛辛苦苦写的好几十篇博文就可能毁于一旦. 所以备份是很重要的. 那么要备份到哪呢? 这里我推荐 Github , 方便快捷, 而且不怕跑路.
初始化首先, 进入博客根目录执行
1git init
然后就会在目录下生成一个 .git 文件.
创建 Github 仓库进入你的 Github , 新建一个仓库, 复制该仓库的 SSH url .
添加远程仓库回到博客根目录, 执行
1git remote add origin git@github.com:xxx/xxx // 即你的 SSH url
然后
123git add * // 这一步可能会报错, 如果报错换成 `git add * -f` 再试试git commit -m "想写啥就写啥, 反正不能不写"git push origin master // 如果报错, 可以直接强制 push 即 `git push -f origin master`
然后你就发现 Github 仓库多了你的源文件.
设置 ...
Valine 评论回复发送重置密码邮件
更新: Valine 新版已经停用了邮件提醒功能.
问题在 Valine 评论系统中留下邮箱后, 回复会发送一份邮件到留下的邮箱. 这本来是评论通知功能, 但是却发送了重置 LeanCloud 密码的邮件?
原因其实原因就在于, Valine 的评论通知功能是基于 LeanCloud 发送重置密码的邮件功能的, 所以才会发送重置密码的邮件.
解决方法进入 LeanCloud 控制台, 修改邮件模板.
改为
1234567你在 {{appname}} 的评论收到了新的回复<p>Hi, {{username}}</p><p>你在 {{appname}} 的评论收到了新的回复,请点击查看:</p><p><a href="你的站点" style="display: inline-block; padding: 10px 20px; border-radius: 4px; back ...
Gamma 函数详解
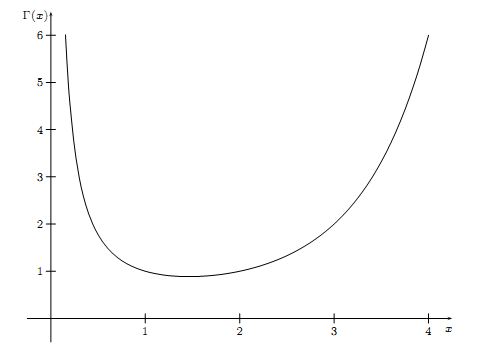
简介 $\mathrm{Gamma}$ 函数如下定义$$
\Gamma(x) = \int_0^{\infty}t^{x - 1}e^{-t}\,\mathrm{d}t
$$那么它是如何来的呢?
考虑如下的一个数列$$
a_n = \{1, 4, 9, 16, \cdots\}
$$这个数列可以用通项公式 $n^2$ 来表达, 即使 $n$ 为实数也是良好定义的. 现在我们来考虑阶乘 $n!$ . 在 $n$ 为整数时, 它是良好定义的, 但是当 $n$ 为实数时呢? $0.5!$ 等于多少? 欧拉于 1729 年完美的解决了这个问题, 由此导致了 $\mathrm{Gamma}$ 函数的产生. $\mathrm{Gamma}$ 函数可以看作是定义在实数域的 $(n - 1)!$ 为什么不是 $n!$ 呢? 后面会说明.
欧拉考虑了如下形式的积分 (至于为什么是如下形式的积分, 请自行了解).$$
J(e,n) = \int_0^1 x^e(1 - x)^n\,\mathrm{d}x
$$这里的 $e$ 并不是自然对数的底数, 而是任意实数. 由分布积分可得$$
\begin ...
git clone 速度太慢? 一招教你加速 git (效果显著)
在天朝, 由于众所周知的原因, git clone github 仓库的速度非常的慢, 所以这里就介绍一个加速 git 的方法.
fork 仓库如果是自己的仓库可以跳过, 如果要 git clone 别人的仓库, 那就先 fork 到自己的 github 仓库中.
注册码云首先注册一个码云账号 (可以用 github 账号登陆) , 点此进入.
点击 从 GitHub/GitLab 导入仓库
找到你要 git clone 的仓库, 然后导入.
git clone 码云仓库成功导入后, 进入你已经导入成功的码云仓库, 然后使用 https 方式 clone.
然后你就会发现…简直是飞速!!!
如果想要 git push 到 github 而不是码云, 那么只要更改远程仓库地址为 github 就好了.
hexo d 命令后 github 无法更新问题
问题hexo d 后查看仓库, 发现根本没有更新, 仔细观察 shell 的输出, 还会看到如下报错
1Branch master set up to track remote branch master from git@github.com:xxxx/xxxx.github.io.git.
其中 xxxx 是你的 github 用户名.
解决方案删除 hexo/.deploy_git 文件, 然后重新尝试 hexo d , 就可以成功更新了.
这应该不算水文吧.
读懂西瓜书 14 : 概率图模型
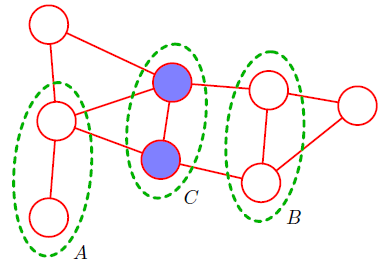
马尔可夫性本章最重要的概念就是马尔可夫性. 马尔可夫性是指变量的状态只与其前一个时刻的状态有关, 而与其他的状态无关, 称为 “无后效性” . 这里可以作一个拓展, 即指变量的状态只与其周围的变量状态有关, 这里的 ‘周围’ 既可以是时间也可以是空间.
隐马尔可夫模型隐马尔可夫模型包括两条链, 一条是由可观测的状态组成的, 一条是由不可观测的状态 (隐变量) 组成的. 那么究竟是什么呢, 我们举个例子.
假设每天的天气只与前一天的天气有关. 比如今天如果是晴天, 那么明天有 $70\%$ 的可能还是晴天, 有 $30\%$ 的可能是阴天. 如果今天是阴天, 那么明天有 $50\%$ 的可能是晴天, 有 $50\%$ 的可能还是阴天. 一天只能有一种天气, 所以我们每天都能观测到一种天气, 这是可观测的. 比如经过一个星期, 我们得到了天气关于时间的一个序列
1
2
3
4
5
6
7
晴
晴
晴
阴
阴
晴
晴
现在假设你有个朋友在国外, 你想要知道他们那边的天气, 但是你只了解你的朋友是在家里还是外出, 并不知道具体天气如何, 而且你还知道假如是晴天, 那么他 ...
优化算法汇总
许多机器学习算法都是为了找到损失函数的最小值, 而损失函数是一个关于参数 $$w$$ 的函数. 但是很多算法并没有闭式解, 因此需要优化算法来帮助找到最小值. 这篇博文并不详细讲解优化算法, 只作简单介绍.
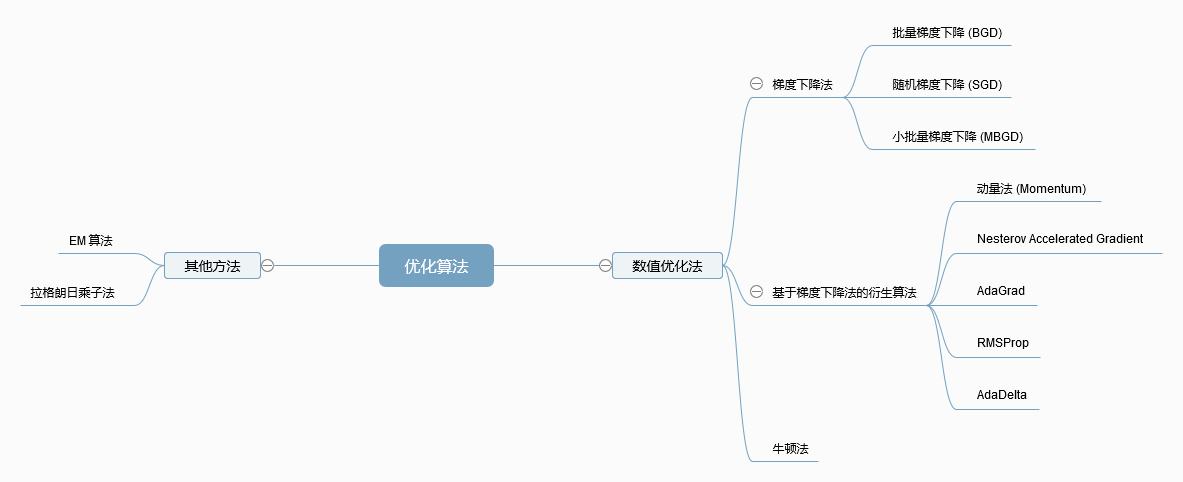
优化算法
数值优化法
梯度下降法
批量梯度下降 (BGD)
随机梯度下降 (SGD)
小批量梯度下降 (MBGD)
基于梯度下降法的衍生算法
动量法 (Momentum)
Nesterov Accelerated Gradient
AdaGrad
RMSProp
AdaDelta
牛顿法
其他方法
EM 算法
拉格朗日乘子法
数值优化法梯度下降法
批量梯度下降 (BGD)批量梯度下降大概是最经典的优化算法之一吧, 也是很多人入门机器学习学的第一个优化算法. 梯度下降的原理就在于 “梯度” , “梯度” 就是函数变化率最大的方向, 一直向着梯度的反方向 “行走” , 值就会变得越来越小, 直到梯度为 0 才停止, 此时则达到了最小值 (可能是局部最小值与全局最小值, 或是鞍点) .
随机梯度下降 (SGD)如果数据集过大, 那么每次计算梯度都需要遍历整个数据 ...
《机器学习》 西瓜书实例 第 7 章: 贝叶斯分类器
《机器学习》 西瓜书的代码实现.
《机器学习》 西瓜书实例 第 7 章
/*!
*
* Twitter Bootstrap
*
*/
/*!
* Bootstrap v3.3.7 (http://getbootstrap.com)
* Copyright 2011-2016 Twitter, Inc.
* Licensed under MIT (https://github.com/twbs/bootstrap/blob/master/LICENSE)
*/
/*! normalize.css v3.0.3 | MIT License | github.com/necolas/normalize.css */
html {
font-family: sans-serif;
-ms-text-size-adjust: 100%;
-webkit-text-size-adjust: 100%;
}
body {
margin: 0;
}
article,
aside,
details,
figcaption,
figure,
foot ...
棋类游戏有必胜策略吗
现在在棋类游戏这方面, AI 已经完胜人类. 即使是最复杂的围棋, 人类也败下阵来. 那么, 是否存在一种策略, 使得黑方或白方必胜呢. 如果这种策略存在, 那么棋类游戏还有其存在意义吗?
策梅洛 (Zermelo) 定理在 1913 年, 策梅洛 (Zermelo) 证明了策梅洛定理, 定理表示在二人的有限游戏中,如果双方皆拥有完全的资讯, 并且运气因素并不牵涉在游戏中, 那先行或后行者当中必有一方有必胜/必不败的策略. 若运用至国际象棋, 则策梅洛定理表示 “要么黑方有必胜之策略、要么白方有必胜之策略、要么双方也有必不败之策略” .策梅洛的论文于1913年以德文发表, 并被 Ulrich Schwalbe 和 Paul Walker 于1997年译为英文.很明显棋类游戏符合上述 “有限游戏”, “拥有完全资讯”, “不包括运气因素” 的要求, 因此是存在必胜或不败的策略的.
证明最让我惊奇的是这条定理的证明如此简单, 只需利用数学归纳法.首先我们定义这个有限游戏的结局, 即黑方胜, 白方胜, 以及平局, 规定在游戏开始后第 m 步如果没有分出胜负则是平局.我们先考虑差一步就可以得到 ...