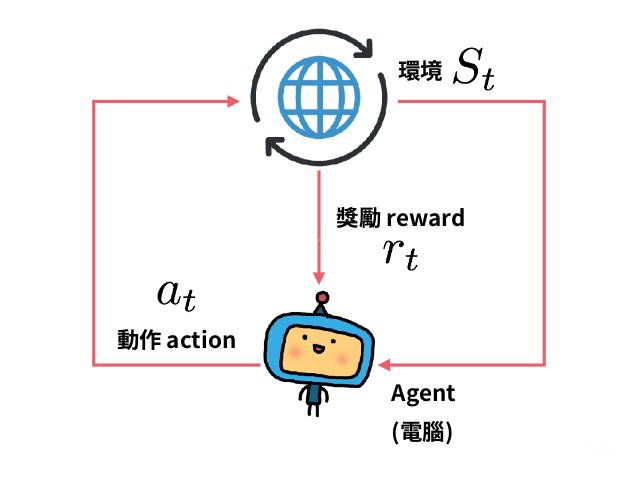
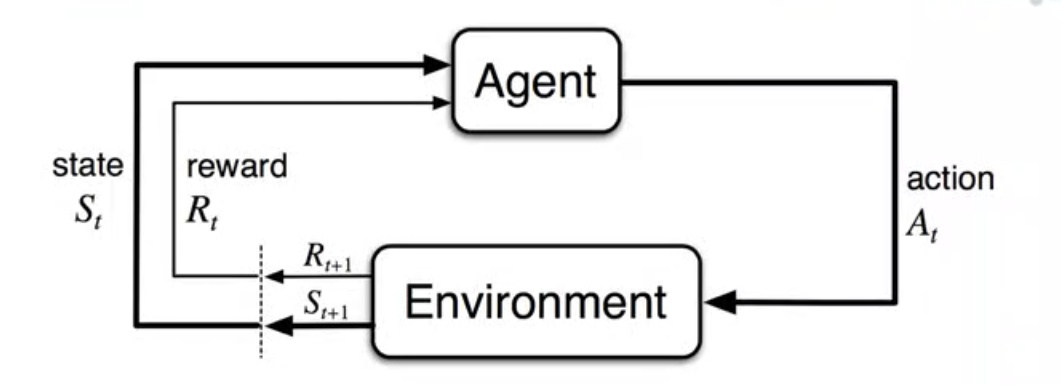
RL 基本概念
两种回报函数在强化学习中, 有两种常用的回报函数, 即有限无折损回报 ($\textrm{finite-horizon undiscount return}$) , 它将有限时间内每个时刻的奖赏加起来作为总回报:$$
R(\tau)=\sum_{t = 0}^Tr_t
$$与无限有折损回报 ($\textrm{infinite-horizon discount return}$) , 将往后至无穷的时间内每个时刻的奖赏加权后求和作为总回报.$$
R(\tau) = \sum_{t = 0}^\infty\gamma^tr_t
$$其中 $\gamma\in(0,1)$ , 是一个参数.
有限无折损回报很容易理解, 那么为什么会有无限有折损回报这种形式呢? 这有着直觉和数学上的双重意义.
直觉上, 我们会将眼前利益看得更重要, 而未来的利益则显得没那么重要 ($\textrm{Cash now is better than cash later}$) .
数学上, 无限无折损回报会无法收敛到一个有限的值, 而乘上 $\gamma^t$ 这个折扣因子 ($\textrm{discount ...
仅引入 JS 实现博客 CDN 加速
前提博客 cdn 加速网上有很多的教程, 其中免备案, 最好用的就是 Jsdelivr 了, 我也写过一篇用 Jsdelivr 加速的文章, 但是似乎很多人一开始都看不懂如何用 Jsdelivr 加速… 这篇文章的原理也是基于 Jsdelivr 加速博文图片, 但是保留了原来的相对路径. 并且能够仅引入一个 JS 实现 Jsdelivr 加速 .
本文的方法只能实现博文内图片加速, 其余页面的图片无法加速 (为了避免与友链图片等冲突, 并且像文章封面这种图片难以只用 JS 实现替换为 Jsdelivr 链接) .
本文能够成功的前提是图片在原文中用相对路径引用, 同时博客部署在 Github 上.
本文的方法可能和懒加载有冲突, 因此建议关闭懒加载 (实际上使用了 Jsdelivr 后加载是飞速的, 根本不需要懒加载) .
除 Butterfly 主题外, 其他主题的 JS 代码并没有经过严格的测试, 因此可能出现 Bug , 请及时留言.
由于主题版本的原因, JS 代码可能会出错或者失效, 请及时留言.
JS 代码为了方便小白, 这里把部分主题 JS 代码写法都写出来了 ...
强化学习入门 Demo
Q Learning12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091import numpy as npimport pandas as pdimport timeimport IPythonlength = 4 # 道路长度epsilon = 0.9 # 贪心值a = [0, 1] # 动作Q_a = np.zeros([length + 1, len(a)]) # Q-a表alpha = 0.1gamma = 0.9game_over = False # 一轮游戏是否结束def print_environment(state): """打印环境""" str = '-' * state ...
读懂西瓜书 16 : 强化学习
K-摇臂赌博机探索与利用探索与利用总是矛盾的, 要使奖赏最大, 就要在探索与利用之间做好权衡.
ϵ-贪心以 $\epsilon$ 的概率进行探索, 以 $1-\epsilon$ 的概率进行利用.
增量式计算令 $Q(k)$ 记录摇臂 $k$ 的平均奖赏. 若摇臂 $k$ 被尝试了 $n$ 次, 得到的奖赏是 $v_1,v_2,\dots,v_n$ , 则平均奖赏为$$
Q(k)=\frac{1}{n}\sum_{i=1}^nv_i
$$由于如果这样计算的话, 需要记录 $n$ 个奖赏值, 算法效率也不高 ( $\mathcal O(n)$ ) , 所以采用增量式计算.$$
\begin{aligned}
Q_n(k)&=\frac{1}{n}\big((n-1)\times Q_{n-1}(k)+v_n\big)\\\\
&=Q_{n-1}(k)+\frac{1}{n}\big(v_n-Q_{n-1}(k)\big)
\end{aligned}
$$这样就只需要记录两个值: 已尝试次数 $n-1$ 以及最近平均奖赏 $Q_{n-1}(k)$ . 算法复杂度也下降到 $\mathcal ...
强迫症的 LaTeX
这篇博文写了一些关于数学公式的规范. 为啥写这个呢, 因为规范了自己数学公式的写法, 才能更有效率的写数学公式. 当然这篇博文不会把所有标准都列出来, 只是强调一些比较小的点. 当然这里所说全部都是 $\mathrm{Markdwon}$ 中的 $\LaTeX$ 公式, 也可以说成是 $\mathrm{MathJax}$ , 所以请大佬们轻喷.
积分正确的积分写法应该是
1\int f(x)\,\mathrm{d}x
$$
\int f(x)\,\mathrm{d}x
$$
即 $\mathrm{d}x$ 与被积函数之间要有一个小小的间隔 \, , 并且 $\mathrm{d}$ 要用正体.
cdots 还是 ldots ?正确的用法是
11+2+3+\cdots+n
$$
1+2+3+\cdots+n
$$
11,2,3,\ldots,n
$$
1,2,3,\ldots,n
$$
即省略号要和它们两边的符号等高. 不过还有一个方便的命令, 即 \dots , 它可以判断应该用哪个省略号.
121+2+3+\dots+n\\\\1,2,3,\dots,n
$$
1+ ...
LDA 详解
先验知识Gamma 函数
Gamma 函数详解
Beta/Dirichlet 分布与共轭
Beta 函数, Beta 分布详解
MCMC, 吉布斯采样这块资料暂时自己去找, 等我有空写了 $\textrm{MCMC}$ 的教程再补上.
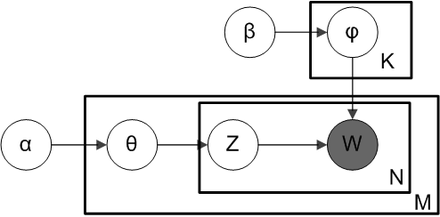
LDA 介绍构成 $\textrm{LDA (Latent Dirichlet Allocation)}$ 是一种词袋模型. 由语料, 文档, 话题. 词, 这三个概念组成.
语料
语料是文档的集合.
文档
文档是词的集合, 可以看做是一篇作文, 或是像这篇一样的博文, 反正就是一篇完整的文本.
话题
话题给出了某个词出现的概率. 到底是啥呢? $\textrm{LDA}$ 认为, 文档中每个词都应该有它的话题, 词是由话题来生成的. 比如说某个词的话题是 “概率论” , 那么这个词就很有可能是 “$\textrm{Gamma}$ 函数” , 而不太可能是 “吃饭” . “可能” 与 “不太可能” 在数学上用概率描述, 而话题就给出了这个概率的值.
词
这应该无需多解释, “词” 本身就是一个词. 文档是由一个个词组成的
生成 ...
Valine 评论回复增强
由于 Valine 本身的评论回复并不是很好用, 而且现在的版本甚至已经取消了评论回复的功能, 因此我们需要 Valine-Admin 来增强.
部署首先我推荐使用国际版的 LeanCloud 而不是华东华北节点 (不用身份证绑定域名也不用备案啥的) , 将数据迁移到国际版可以用 LeanCloud 的数据导入导出功能实现, 不过要注意导出功能只能在中午 12 点前使用.
进入你原本的 Valine 评论的 LeanCloud 应用, 选择 云引擎 -> 部署 -> 部署项目 -> Git 源码部署 -> 配置 Git 中填入 https://github.com/DesertsP/Valine-Admin.git , 然后保存.
分支或提交 填入 master , 然后点击部署
第一次部署需要一点点时间.
配置接下来就是配置了. 进入 云引擎 -> 设置 界面配置环境变量.
变量
值
说明
SITE_NAME
网站名称
SITE_URL
网站地址
SMTP_USER
SMTP 用户名 (一般为你的邮箱)
SMTP ...
解决 Hexo 本地搜索 search.xml 文件加载过慢
问题由于不想使用第三方, 我使用了本地搜索. 但是本地搜索带来的一个问题是, search.xml 太大了, 加载速度缓慢. 如果我们将 search.xml 文件使用外链引用 (例如用 Jsdelivr 加速过的链接) , 就可以解决这个问题.
解决打开主题下的 local-search.js 文件 (不同主题的位置会不同, 但是一般都在 source/js 这种文件夹里) , 找到如下字段
1url: GLOBAL_CONFIG.root + path
改成
1url: 外链
外链推荐使用 Jsdelivr 的 cdn (引用 Github 的资源, 不需要手动更新, 速度也挺快) . 如果你的博客部署在 Github Pages, 那么就可以改成如下形式
1
如果你还不知道什么是 Jsdelivr , 可以看我的这篇文章.
换了外链后, 速度明显增加, 几乎是秒加载.
Butterfly 主题魔改记录
记录下我对 Butterfly 主题的魔改, 一方面可供参考, 另一方面可以记录下自己的修改方便查找.
本博客已开源! 请看 Hexo modify theme butterfly. 以下魔改部分集合到魔改主题, 部分已放弃 (不兼容或者其他原因). 如果更改失效, 可能是版本问题, 如果想要尽快使用这些魔改, 最便捷的方式是直接使用我的魔改主题. 魔改主题保留了所有原配置, 所有魔改配置均可关闭.
Mathjax 公式渲染去除滚动条进入 source/css/_layout/third-party.styl , 找到如下内容
12.has-jax overflow: auto
改成
12.has-jax overflow: visible
设置半透明效果看我博客.
进入source/css/_layout/page.styl 文件, 找到以下内容
123456.layout_page display: flex align-items: flex-start margin: 0 auto padding: 2rem 15px max-width: 1200px
后面 ...
Beta 函数, Beta 分布详解
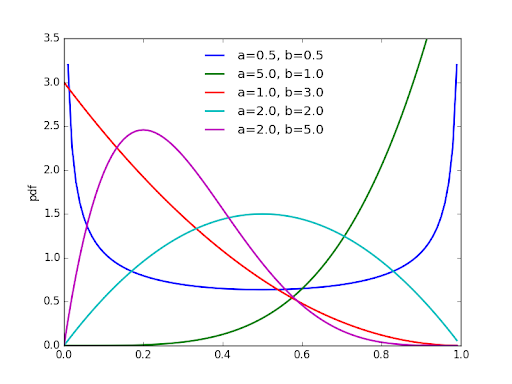
推导第一种 $\mathrm{Beta}$ 分布一般被用于建模伯努利试验事件成功的概率的概率分布. 什么叫做伯努利试验事件成功的概率? 我们来举个例子.
如果有一枚硬币, 分为正反两面 (不一定均匀) , 那么假设你抛了 $10$ 次, 正面有 $7$ 次, 那么抛这枚硬币是正面的概率是多少呢? 当然我们一般会说是 $7/10$ , 但这只是最好的估计. 可能是 $1/10$ 吗? 当然可能, 但是可能性不高. 这里的 $7/10$ , $1/10$ 就是所谓伯努利试验事件成功的概率. 而其服从的分布就是伯努利试验事件成功的概率的概率分布.
二项分布相信大家高中就都已经接触过了$$
P(x) = \binom{n}{x}q^x(1-q)^{n-x}
$$这是已知参数 $n, q$ 来估计 $x$ , 我们同样可以将其等价地写为 $P(x\mid q)$ . 那如果我们知道了 $n,x$ , 要如何估计 $q$ 呢? 也就是如何求出 $P(q\mid x)$ (省略了 $n$ 是为了方便写公式, 毕竟两个条件概率都是已知 $n$ 的) .
根据贝叶斯公式, 我们有$$
P ...