优化算法汇总

许多机器学习算法都是为了找到损失函数的最小值, 而损失函数是一个关于参数

$$w$$

的函数. 但是很多算法并没有闭式解, 因此需要优化算法来帮助找到最小值. 这篇博文并不详细讲解优化算法, 只作简单介绍.

• 优化算法
  • 数值优化法
    • 梯度下降法
      • 批量梯度下降 (BGD)
      • 随机梯度下降 (SGD)
      • 小批量梯度下降 (MBGD)
    • 基于梯度下降法的衍生算法
      • 动量法 (Momentum)
      • Nesterov Accelerated Gradient
      • AdaGrad
      • RMSProp
      • AdaDelta
    • 牛顿法
  • 其他方法
    • EM 算法
    • 拉格朗日乘子法

数值优化法

梯度下降法

批量梯度下降 (BGD)

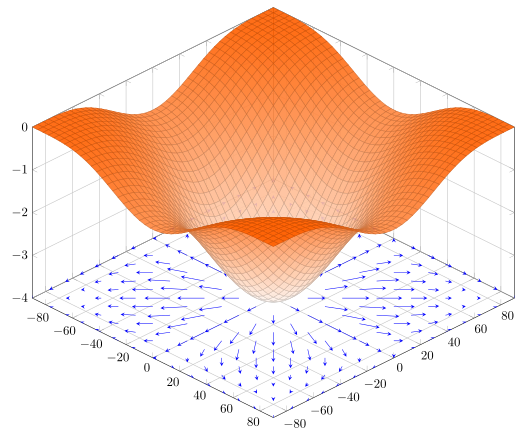
批量梯度下降大概是最经典的优化算法之一吧, 也是很多人入门机器学习学的第一个优化算法. 梯度下降的原理就在于 “梯度” , “梯度” 就是函数变化率最大的方向, 一直向着梯度的反方向 “行走” , 值就会变得越来越小, 直到梯度为 0 才停止, 此时则达到了最小值 (可能是局部最小值与全局最小值, 或是鞍点) .

随机梯度下降 (SGD)

如果数据集过大, 那么每次计算梯度都需要遍历整个数据集, 这样消耗的时间太久, 导致训练过慢, 由此引进了随机梯度下降. 随机梯度下降每次训练只使用一个数据, 大大加快了计算梯度的效率, 同时, 还可以跳出局部最小值. 但是也导致了一个问题, 就是每次下降的方向都不一定是最优的, 甚至可能往反方向进行, 因此较难收敛, 为了解决这个问题, 产生了 $\mathrm{mini}-\mathrm{batch}(\mathrm{MBGD})$ .

小批量梯度下降 (MBGD)

 $\mathrm{MBGD}$ 结合了 $\mathrm{BGD}$ 和 $\mathrm{SGD}$ 的优点, 一次只训练一小部分训练集, 即保证了梯度的方向大致是正确的, 又保证了更新的速度. 算是一种折中的做法, 效果也是很不错.

基于梯度下降法的衍生算法

动量法 (Momentum)

有时候, 某些方向的梯度过大时, 那么就有可能造成震荡, 导致收敛过慢, 甚至无法收敛. 由此引进了动量法.

动量法通过对历史梯度进行指数加权来平滑优化轨迹, 如果历史梯度与当前相反 (也就是说会 “震荡”) , 那么就会相应减少步长, 以达到 “平滑” 的目的.

Nesterov Accelerated Gradient

动量法的改进算法, 可以看作是更 “高瞻远瞩” 的动量法, 性能比动量法好很多.

AdaGrad

动量法是通过改变步长来防止发散, 而 $\mathrm{AdaGrad}$ 是通过给不同的变量赋予不同的、动态变化的学习率来防止发散. 其原理是根据历史梯度的绝对值来降低学习率 (降低的大小不同), 直观上来看, 如果历史梯度绝对值一直比较大, 就会降低学习率. 但是由于降低的过程是一直累加, 所以到训练后期学习率会过小, 难以产生有用的解, 因此又产生了它的改进算法: $\mathrm{RMSProp}$ 与 $\mathrm{AdaDelta}$ .

RMSProp

 $\mathrm{RMSProp}$ 和 $\mathrm{AdaGrad}$ 的区别在于, $\mathrm{AdaGrad}$ 对历史梯度是一直累加, 而 $\mathrm{RMSProp}$ 是通过指数加权历史梯度来防止步长过小.

AdaDelta

 $\mathrm{AdaDelta}$ 又对 $\mathrm{RMSProp}$ 作了进一步的改进, 将参数 $\mu$ 也用指数加权替代了.

牛顿法 (Newton Method)

牛顿法是对泰勒展开的应用. 一般比梯度下降收敛的速度要快很多. 但是对于多维变量, 由于要求矩阵的二阶导 (也就是 $\mathrm{Hessen}$ 矩阵) , 所以会比较麻烦.

其他方法

EM 算法

 $\mathrm{EM}$ 算法一般用来估计隐变量, 总结一句话: 我 迭 代 我 自 己.

拉格朗日乘子法

拉格朗日乘子法通过引入拉格朗日乘子, 可将有 $d$ 个变量与 $k$ 个约束条件的最优化问题转化为具有 $d+k$ 个变量的无约束优化问题求解.