(史济怀) 数学分析教程上册第 3 版-练习题 1.1
1用反证法. 假设 $a+b$ 是有理数, 那么有 $a+b = \frac{p}{q}$ , 令 $a=\frac{p'}{q'}$ , 那么有$$
\begin{aligned}
\frac{p'}{q'} + b &= \frac{p}{q}\\
b&=\frac{pq'-p'q}{qq'}
\end{aligned}
$$即 $b$ 为有理数, 与题目矛盾, 因此 $a+b$ 是无理数. $a-b$ 是同理可得.
若 $ab$ 是有理数, 那么有 $ab = \frac{p_0}{q_0}$ , 因此 $b=\frac{p_0}{aq_0}$ , 即 $b$ 为有理数, 矛盾, 因此 $ab$ 是无理数. $a/b$ 同理可得.
2这里只考虑大于零的情况 (小于等于零的情况类似, 因此为了方便不做讨论) . 假设有两个有理数 $a=\frac{p}{q}>b=\frac{p'}{q'}>0$ . 通分得 $\frac{pq'}{qq'}>\frac{p'q}{qq'}$ , 显然有 $\frac{pq'-1}{qq'}\geqslant\frac{p'q}{qq'}$ , 等 ...
(史济怀) 数学分析教程上册第 3 版-练习题 1.3
1(1)不能.
(2)发散.
(3)发散.
(4)既可以收敛也可以发散.
(5)$\{a_n\},\{b_n\},\{c_n\}$ 都不一定收敛.
# 2
对于 $\epsilon'>0$, 存在 $N\in\mathbb{Z}^*$ , 使得当 $n>N$ 时, 有 $|a_n-a|
一个问题
说在前面这个问题我还没有解决.
题目已知平面向量 $v_1,v_2,v_3,\cdots,v_n$ 满足 $\sum_{i=1}^n|\vec{v_i}|=1$ . 若必存在若干个向量, 它们的和的模不小于 $k$ , 求 $k$ 的最大值.
原题如下
给出的解法虽然很精彩, 但是并不是最大值 (最少是没证明 $1/4$ 是最大值) . 于是就产生了这个求最大值的想法.
猜想我猜测结果是 $1/\pi$ .
一些结果令 $P\subseteq \{1,2,3,\cdots,n\}$ , 且满足 $\left|\sum_{i\in P}v_i\right|$ 为所有向量相加的组合中能取到的最大值, 我们来考虑如何选取得到这个向量的集合. 设一个向量 $\vec{w}\not=\vec 0$ , 如何取向量并相加才能使得这个相加后的向量在 $\vec{w}$ 上的投影的模最大? 很显然, 取一条过原点的直线, 然后分别将直线的两边的所有向量相加 (在直线上的向量相加与否并不影响这个模的取值), 得到的两个向量必有一个在 $\vec{w}$ 上的投影的模是最大的, 但是这样取到的最大的模必 ...
一个不等式
发现一个不等式, 因此记录一下 (应该是正确的…吧)$$
\sum_{i=1}^nk_i\sin(\theta_i)\geqslant\frac{\sqrt{2}}{2}\sin\left(\frac{\sum_{i=1}^nk_i\theta_i}{\sum_{i=1}^nk_i}\right)\sum_{i=1}^n k_i,\qquad \theta_i\in[0,\frac{\pi}{2}]
$$对于 $\cos$ 函数也有类似的结果.
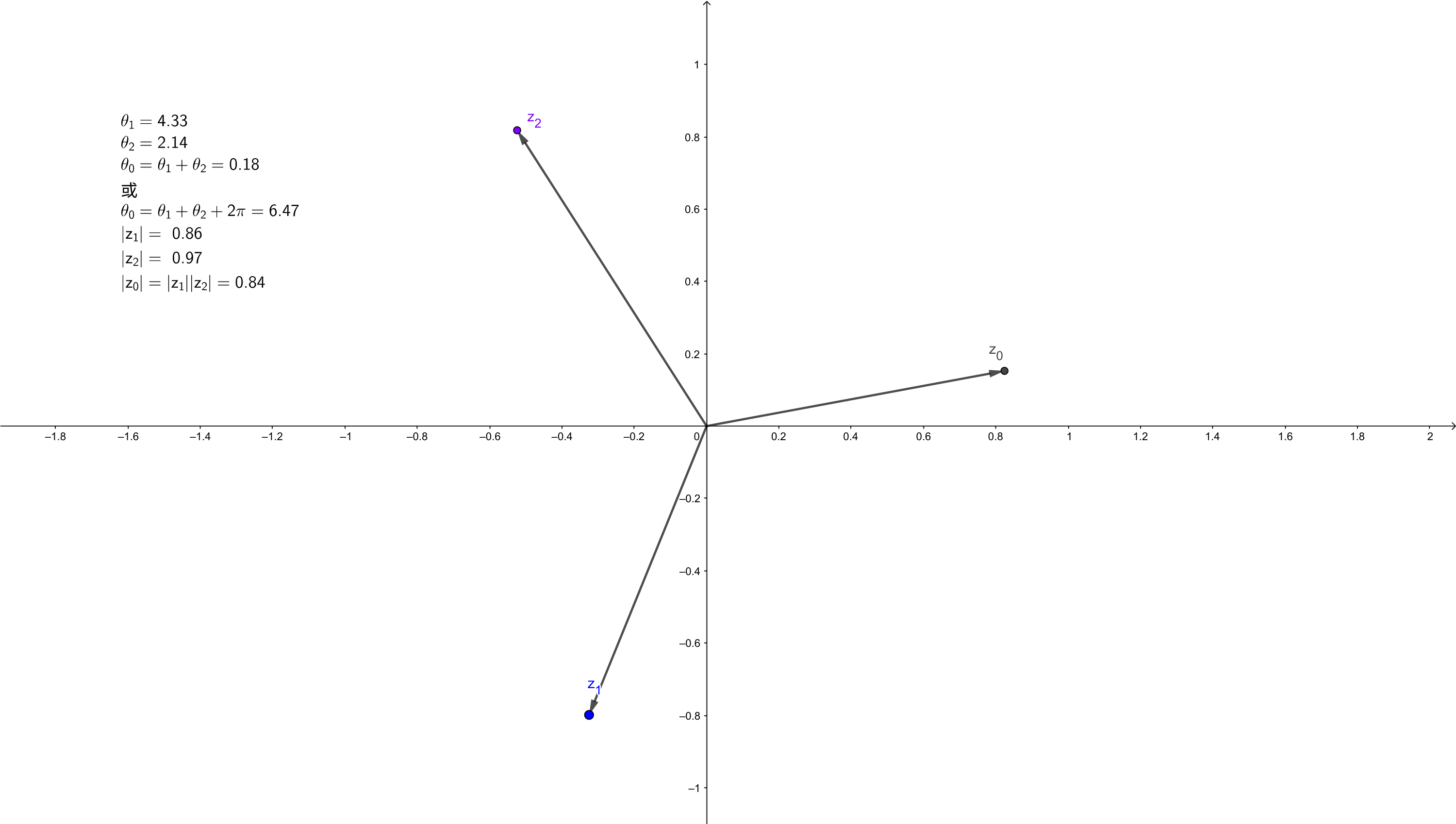
复数乘法与旋转
旋转公式对于一个点 $P_0(x_0,y_0)$ 来说 , $P_1(x_0\cos\theta-y_0\sin\theta,x_0\sin\theta+y_0\cos\theta)$ 是 $P_0$ 旋转 $\theta$ 角度 (顺时针) 后对应的点. 这个公式的推导是很简单的, 但是它这样的形式似乎并没有什么显而易见的规律. 但是, 复数乘法可以给我们一些启示.
复数乘法的几何意义设 $z_1=a_1+b_1\mathrm{i}, z_2=a_2+b_2\mathrm{i}$ , 那么就有 $z_1z_2=a_1a_2-b_1b_2+(a_1b_2+a_2b_1)\mathrm{i}$ . 如果还看不出什么, 就进行三角换元, 令 $a_1=k_1\cos\alpha, b_1=k_1\sin\alpha, a_2=k_2\cos\beta,b_2=k_2\sin\beta$ , 那么就有 $k_1=|z_1|, k_2=|z_2|$ , 于是$$
\begin{aligned}
z_1z_2&=a_1a_2-b_1b_2+(a_1b_2+a_2b_1)\mathrm{i}\\
...
在网页中嵌入 GGB 最简单的方法
一开始我是想要用官网的 js 解析 .ggb 文件的, 结果发现速度太慢还一堆问题… 最后发现直接分享然后 iframe 引用才是最快最方便的.
打开 GeoGebra , 然后在制作好的图中点击分享 (如下图)
然后就会进入登录界面, 有账号直接登录, 没有就注册.
接着进入 GGB 官网 , 登录并进入个人主页
接着看 资源 中是否有你分享的图, 如果没有, 重新回到 GGB 再次尝试分享.
然后点击进入你要嵌入到网页的资源, 查看该资源 ID .
记下 ID, 然后就可以在需要展示 GGB 的地方用 iframe 引用了
1234567<iframe frameborder="no"title="随便写" src="https://www.geogebra.org/material/iframe/id/刚刚记下的 ID/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false/" ...
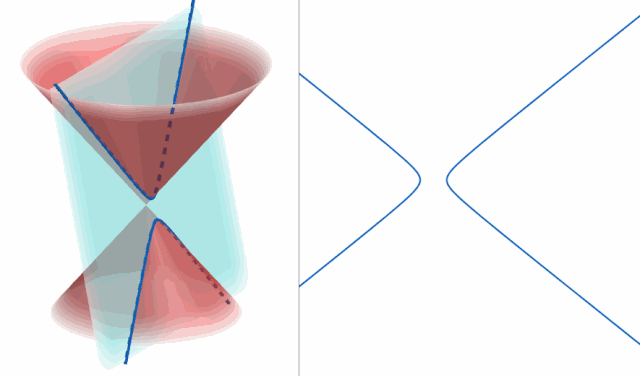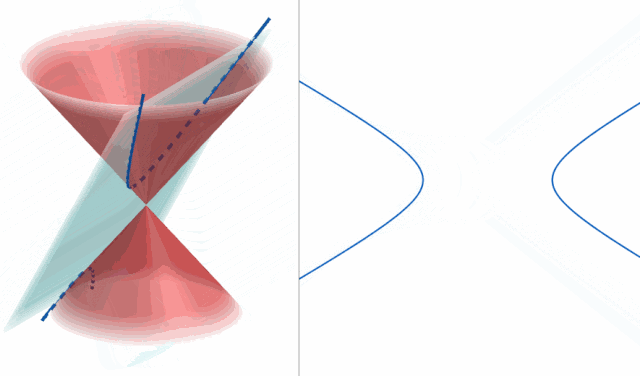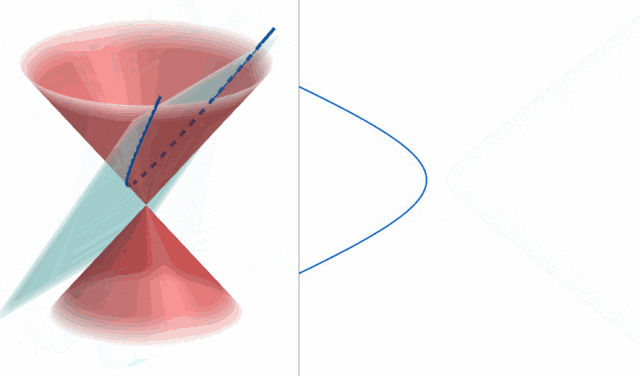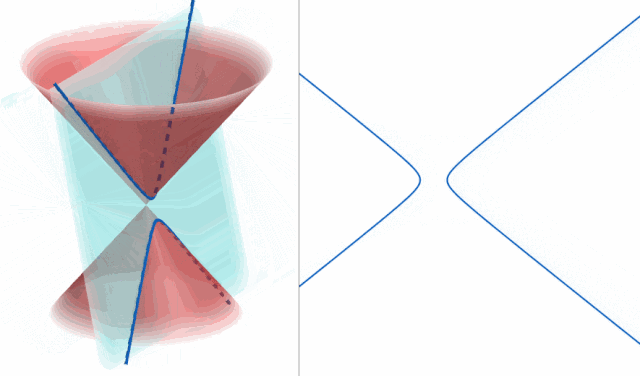
圆锥曲线二级结论
最近推了一个圆锥曲线的结论, 因此记录一下.
先上结论:
若有圆锥曲线 $\Gamma\colon\frac{x^2}{A}+\frac{y^2}{B}=1$ ,$A$ 与 $B$ 不同时取负数 (这样就同时代表了双曲线和椭圆) , 那么对于一个在该圆锥曲线上的点 $P_1(x_1,y_1)$ 来说, 存在一个点 $P_2(\frac{A-B}{A+B}x_1,\frac{B-A}{A+B}y_1)$ . 若作直线 $l_1, l_2$ 过点 $P_0$ 且相互垂直, 那么这两条直线与该圆锥曲线异于 $P_0$ 的两个交点 $M,N$ 的连线恒过点 $P_1$ .
对于形如 $y^2=2px$ 的抛物线也有类似结论, 不过 $P_2$ 为 $(2p+x_1,-y_1)$.
如何得到我们以椭圆为例.
设椭圆 $\Gamma\colon\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ , 点 $P_2 (x_2, y_2)$ , 直线 $l_{MN}\colon y-y_2=k(x-x_2)$ 联立可得$$
(a^2k^2+b^2)x^2+2a^2k ...
解决 MathJax 与 Hexo 冲突问题
将 Hexo 升级到 5.0 后, 发现 MathJax 与 Hexo 仍然有冲突. 然而网上大部分的方法对 5.0 版本的 Hexo 都没有用.
摸索许久后, 找到了一个比较不错的方法解决该问题. 即在公式前后加上 ` 与 `, 即
12345{%raw%}$$xxxxxx (公式内容)$${%endraw%}
就可以完美解决.
这绝对不是水文.
DQN 算法
论文原文: Playing Atari with Deep Reinforcement Learning .
DQN (Deep Q-Networks) 算法, 简单来说就是 Deep Learning + Q Learning.
Q LearningQ Learning 实际上是维护一个 $Q$ 值表, 这个表可以认为是状态 $s$ 与动作 $a$ 的一个函数 $Q(s,a)$ , 其输出表示在状态 $s$ 下采用动作 $a$ 所获得的期望回报. 通过查询 $Q$ 值表, 就可以找出在某个状态 $s_t$ 下的最佳动作 $a_t$ . Q Learning 算法的要点就在于得到一个足够真实的 $Q$ 值表. 而 $Q$ 值表的更新, 则基于 Bellman 方程 (详情可见RL 基本概念).
DQNDQN 的核心思想与 Q Learning 一样, 但区别就在于 $Q$ 函数. 在 Q Learning 中, $Q$ 函数是 $Q$ 值表, 也即一个个状态-动作对与期望回报的一一对应, 也就是离散的, 而在一些环境中 (比如 Atari 2600 games) 状态几乎是无穷多的, ...
为你的博客添加一个播放器
话不多说, 直接开整.
播放器文件下载并引入地址在 https://github.com/cnyist/player .
下载下来后放入 source 目录中 (主题或 Hexo 自带的皆可) , 然后用 iframe 引入 index.html 文件
1iframe(name="player", id="player", src="/player/", frameborder="0", onload="this.width=player.jp_container_N.scrollWidth;{%raw%}$('.songlist__item').each(function(){generate(${%endraw%}(this).attr('id'))});", style="z-index:100; position:fixed; left:0px; bottom:0px")
以上代码建议插入到 head ...